비트코인: P2P 전자 현금 시스템

• 작성자: 사토시 나카모토
• [email protected]
• 백서 다운로드: https://www.bitcoin.org/bitcoin.pdf

초록

순수한 P2P 방식의 전자 현금 시스템은 금융 기관을 거치지 않고 한 당사자로부터 다른 당사자에게 직접 온라인 결제를 보낼 수 있도록 합니다. 디지털 서명은 이 문제의 일부를 해결해주지만, 이중 지불을 방지하기 위해 신뢰할 수 있는 제3자가 여전히 필요하다면 주요 이점이 사라집니다. 우리는 P2P 네트워크를 사용하여 이중 지불 문제에 대한 해결책을 제안합니다. 네트워크는 해시 기반 작업 증명(proof-of-work)을 사용하여 거래를 해싱하고 연속적인 해시 체인에 타임스탬프를 부여함으로써, 작업 증명을 다시 하지 않으면 변경할 수 없는 기록을 형성합니다. 가장 긴 체인은 목격된 사건 순서를 증명할 뿐만 아니라, 가장 큰 CPU 파워 풀이 기여했음을 증명합니다. 전체 CPU 파워의 과반수가 네트워크를 공격하려는 협력 없이 운영된다면, 이들은 가장 긴 체인을 생성하여 공격자를 앞설 것입니다. 네트워크 자체는 최소한의 구조만 필요로 합니다. 메시지는 최선의 노력을 다해 브로드캐스트되며, 노드는 언제든지 네트워크에 떠나고 다시 참여할 수 있고, 자신이 떠나 있는 동안 발생한 일을 가장 긴 작업 증명 체인으로 받아들입니다.

1. 서론

인터넷 상의 상거래는 거의 전적으로 금융 기관이 신뢰할 수 있는 제3자로서 전자 결제를 처리하는 방식에 의존해 왔습니다. 이러한 시스템은 대부분의 거래에서 충분히 잘 작동하지만, 신뢰 기반 모델이 가지는 고유한 약점을 여전히 지니고 있습니다. 금융 기관은 분쟁 중재를 피할 수 없기 때문에 완전히 비가역적인 거래는 사실상 불가능합니다. 중재 비용은 거래 비용을 증가시키며, 실질적으로 가능한 최소 거래 규모를 제한하고 소액의 간단한 거래를 어렵게 만듭니다. 또한, 비가역적인 서비스에 대해 비가역적인 결제를 할 수 없는 손실도 발생합니다. 결제의 취소 가능성 때문에 신뢰가 필요해지고, 상인은 고객이 필요 이상으로 많은 정보를 제공하도록 요구하는 상황이 생깁니다. 일정 비율의 사기는 피할 수 없는 것으로 간주됩니다. 이러한 비용과 결제 불확실성은 대면 거래에서 물리적 화폐를 사용함으로써 피할 수 있지만, 통신 채널을 통해 신뢰할 수 있는 제3자 없이 결제를 수행할 수 있는 메커니즘은 존재하지 않습니다.

필요한 것은 신뢰 대신 암호학적 증거를 기반으로 한 전자 결제 시스템으로, 이를 통해 신뢰할 수 있는 제3자 없이도 두 당사자가 직접 거래할 수 있게 하는 것입니다. 복잡한 계산을 통해 취소가 사실상 불가능한 거래는 판매자를 사기로부터 보호할 수 있으며, 간단한 에스크로 메커니즘을 통해 구매자 보호도 쉽게 구현할 수 있습니다. 이 논문에서는 P2P 분산형 타임스탬프 서버를 사용하여 거래의 시간 순서에 대한 계산적 증거를 생성함으로써 이중 지불 문제를 해결하는 방안을 제안합니다. 이 시스템은 정직한 노드들이 협력하는 공격 노드 그룹보다 더 많은 CPU 파워를 집단적으로 통제하는 한 안전합니다.

2. 거래

전자 화폐를 디지털 서명의 연속 체인으로 정의합니다. 각 소유자는 이전 거래의 해시와 다음 소유자의 공개 키에 디지털 서명을 하고 이를 코인의 끝에 추가하여 코인을 다음 소유자에게 이전합니다. 수취인은 서명을 확인하여 소유권의 연속성을 검증할 수 있습니다.

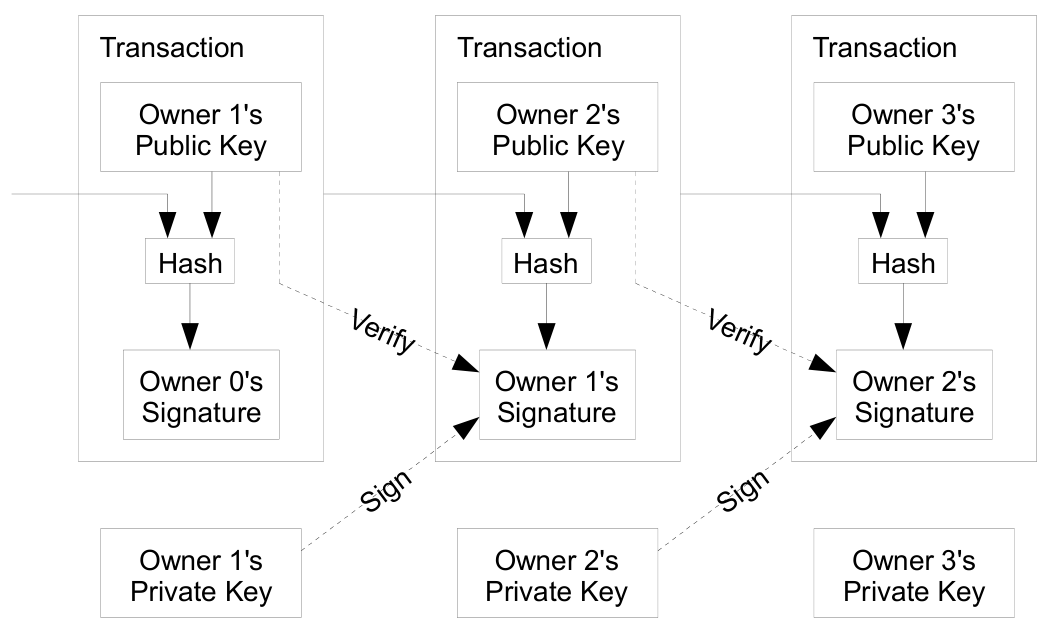
문제는 수취인이 이전 소유자 중 하나가 해당 코인을 이중 지불하지 않았다는 것을 확인할 수 없다는 점입니다. 일반적인 해결책은 모든 거래에서 이중 지불을 확인하는 신뢰할 수 있는 중앙 기관, 즉 발행소를 도입하는 것입니다. 각 거래 후 코인은 발행소에 반환되어 새로운 코인을 발행받아야 하며, 발행소에서 직접 발행한 코인만이 이중 지불되지 않은 것으로 신뢰받습니다. 그러나 이 해결책의 문제는 전체 화폐 시스템이 발행소를 운영하는 회사에 의존하게 된다는 점입니다. 모든 거래가 발행소를 거쳐야 하기 때문에 은행 시스템과 유사한 구조를 갖게 됩니다.

수취인이 이전 소유자들이 다른 이전 거래에 서명하지 않았다는 사실을 알 수 있는 방법이 필요합니다. 우리의 목적상 가장 이른 거래가 유효한 것으로 간주되므로, 이후의 이중 지불 시도는 중요하지 않습니다. 거래가 존재하지 않음을 확인하는 유일한 방법은 모든 거래에 대한 정보를 갖는 것입니다. 발행소 기반 모델에서는 발행소가 모든 거래를 알고 있으며, 어떤 거래가 먼저 도착했는지를 결정했습니다. 신뢰할 수 있는 제3자 없이 이를 달성하려면, 거래가 공개적으로 발표되어야 하며, 참여자들이 거래가 접수된 순서에 대한 단일한 기록에 동의할 수 있는 시스템이 필요합니다¹. 수취인은 각 거래 시점에 과반수 노드가 해당 거래가 최초로 수신된 거래라고 동의했다는 증거를 요구합니다.

3. 타임스탬프 서버

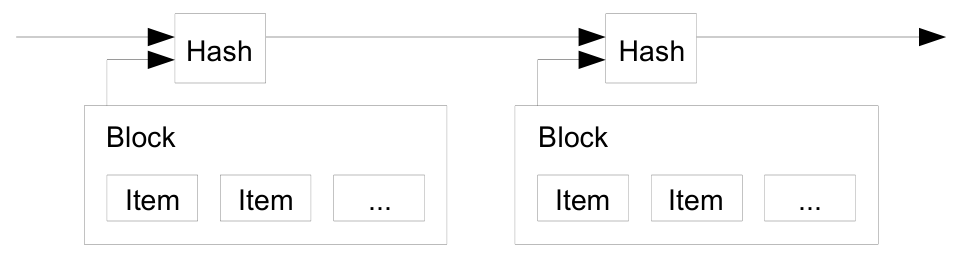
우리가 제안하는 해결책은 타임스탬프 서버에서 시작합니다. 타임스탬프 서버는 타임스탬프를 찍어야 할 항목 블록의 해시를 생성하고, 이를 신문이나 유즈넷 게시물 등에 널리 공개하는 방식으로 작동합니다²³⁴⁵. 타임스탬프는 해당 데이터가 해시에 포함되기 위해서는 그 시점에 존재했어야 한다는 것을 증명합니다. 각 타임스탬프는 이전 타임스탬프를 자신의 해시에 포함하여 체인을 형성하며, 이후에 추가되는 타임스탬프가 앞선 타임스탬프를 더욱 강화하는 구조를 갖습니다.

4. 작업 증명

P2P 방식으로 분산 타임스탬프 서버를 구현하기 위해서는 신문이나 유즈넷 게시물 대신 Adam Back의 Hashcash⁶와 유사한 작업 증명 시스템을 사용할 필요가 있습니다. 작업 증명은 SHA-256과 같은 해시 함수에서 특정 개수의 앞쪽 비트가 0이 되도록 하는 값을 찾는 과정을 포함합니다. 요구되는 0 비트의 수에 따라 필요한 평균 작업량은 기하급수적으로 증가하며, 단일 해시 계산으로 쉽게 검증할 수 있습니다.

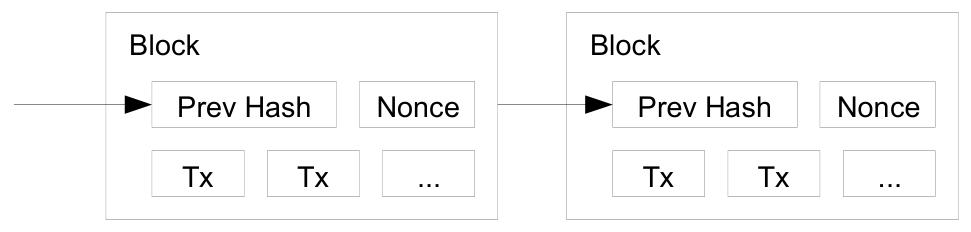
우리의 타임스탬프 네트워크에서는 블록 내에서 논스(nonce)를 증가시키며 블록의 해시가 요구되는 0 비트를 포함하는 값을 찾음으로써 작업 증명을 구현합니다. CPU 자원을 투입하여 작업 증명을 충족하도록 블록을 만들면, 그 작업을 다시 하지 않고는 블록을 변경할 수 없게 됩니다. 이후에 다른 블록들이 체인에 추가됨에 따라, 해당 블록을 수정하려면 이후 모든 블록의 작업을 다시 해야 합니다.

작업 증명은 또한 다수결 결정에서 대표성을 결정하는 문제를 해결합니다. 다수결을 '하나의 IP 주소당 한 표'로 기반할 경우, 많은 IP 주소를 확보할 수 있는 사람이 이를 악용할 수 있습니다. 작업 증명은 본질적으로 ‘하나의 CPU당 한 표’를 의미합니다. 다수결 결정은 가장 긴 체인으로 표현되며, 이는 가장 많은 작업 증명 노력이 투자된 체인입니다. 과반수의 CPU 파워가 정직한 노드들에 의해 통제될 경우, 정직한 체인은 가장 빠르게 성장하여 경쟁 체인을 앞서게 됩니다. 과거의 블록을 수정하려면, 공격자는 해당 블록과 그 이후의 모든 블록에 대해 작업 증명을 다시 수행해야 하며, 정직한 노드들의 작업량을 따라잡고 추월해야 합니다. 이후 블록이 추가됨에 따라 더 느린 공격자가 따라잡을 확률이 기하급수적으로 감소함을 나중에 설명할 것입니다.

하드웨어 속도의 증가와 노드 운영에 대한 관심 변화를 보완하기 위해, 작업 증명의 난이도는 시간당 평균 블록 수를 목표로 하는 이동 평균을 통해 결정됩니다. 블록이 너무 빨리 생성되면 난이도가 증가합니다.

5. 네트워크

네트워크를 운영하는 단계는 다음과 같습니다.

1. 새로운 거래가 모든 노드에 브로드캐스트됩니다.
2. 각 노드는 새 거래를 모아 하나의 블록으로 만듭니다.
3. 각 노드는 자신이 만든 블록에 대해 어려운 작업 증명을 찾기 위해 계산을 수행합니다.
4. 한 노드가 작업 증명을 찾으면 해당 블록을 모든 노드에 브로드캐스트합니다.
5. 노드들은 해당 블록 내의 모든 거래가 유효하고 이중 지불되지 않았을 때에만 블록을 수용합니다.
6. 노드는 수용한 블록의 해시를 이전 해시로 사용하여 체인의 다음 블록을 생성함으로써 해당 블록에 대한 수용을 표현합니다.

노드들은 항상 가장 긴 체인이 올바른 것으로 간주하며 이를 확장하는 작업을 계속합니다. 만약 두 노드가 동시에 다른 버전의 다음 블록을 브로드캐스트하면, 일부 노드는 한 블록을, 다른 일부 노드는 다른 블록을 먼저 받게 될 수 있습니다. 이 경우 노드들은 먼저 받은 블록에 대해 작업을 진행하지만, 다른 분기를 저장하여 그 분기가 더 길어질 경우를 대비합니다. 다음 작업 증명이 발견되어 어느 한 분기가 더 길어지면, 다른 분기에서 작업 중이던 노드들은 더 긴 분기로 전환하게 됩니다.

새로운 거래 브로드캐스트는 반드시 모든 노드에 도달할 필요는 없습니다. 다수의 노드에 도달하기만 하면 머지않아 블록에 포함될 것입니다. 블록 브로드캐스트 또한 메시지 손실에 대해 관용적입니다. 특정 노드가 블록을 받지 못하면, 이후 블록을 수신했을 때 누락된 블록이 있음을 인식하고 해당 블록을 요청하게 됩니다.

6. 인센티브

관례에 따라, 각 블록의 첫 번째 거래는 해당 블록의 생성자가 소유하는 새로운 코인을 시작하는 특별한 거래입니다. 이는 노드들이 네트워크를 지원하도록 하는 인센티브를 제공하며, 중앙 권한이 없는 상태에서 코인을 초기 분배할 수 있는 방법을 제시합니다. 일정한 양의 새로운 코인이 지속적으로 추가되는 것은 금광 채굴자가 자원을 소비하여 금을 유통에 추가하는 것과 유사합니다. 우리의 경우, 이는 CPU 시간과 전기를 소비하는 것입니다.

또한 인센티브는 거래 수수료로도 충당될 수 있습니다. 거래의 출력 값이 입력 값보다 적을 경우, 그 차액은 해당 거래를 포함하는 블록의 인센티브 가치에 추가되는 거래 수수료가 됩니다. 미리 정해진 수의 코인이 유통에 투입된 후에는, 인센티브가 전적으로 거래 수수료로 전환되어 완전히 인플레이션 없는 상태가 될 수 있습니다.

인센티브는 노드들이 정직하게 유지되도록 장려할 수 있습니다. 만약 탐욕스러운 공격자가 모든 정직한 노드보다 더 많은 CPU 파워를 모을 수 있다면, 그는 자신의 결제를 다시 훔쳐가는 방식으로 사람들을 속이거나 새로운 코인을 생성하는 방식 중 하나를 선택해야 합니다. 공격자는 규칙을 따르며 새로운 코인을 얻는 것이 시스템을 훼손하여 자신의 재산의 가치를 떨어뜨리는 것보다 더 수익성이 높다는 결론을 내리게 될 것입니다.

7. 디스크 공간 회수

코인의 최신 거래가 충분한 블록 아래에 묻히면, 이전에 사용된 거래들을 삭제하여 디스크 공간을 절약할 수 있습니다. 이를 블록의 해시를 손상시키지 않고 수행하기 위해 거래들은 머클 트리(Merkle Tree)⁷²⁵로 해싱되며, 블록의 해시에는 트리의 루트만 포함됩니다. 오래된 블록들은 트리의 가지를 잘라내어 압축할 수 있으며, 중간 해시는 저장할 필요가 없습니다.

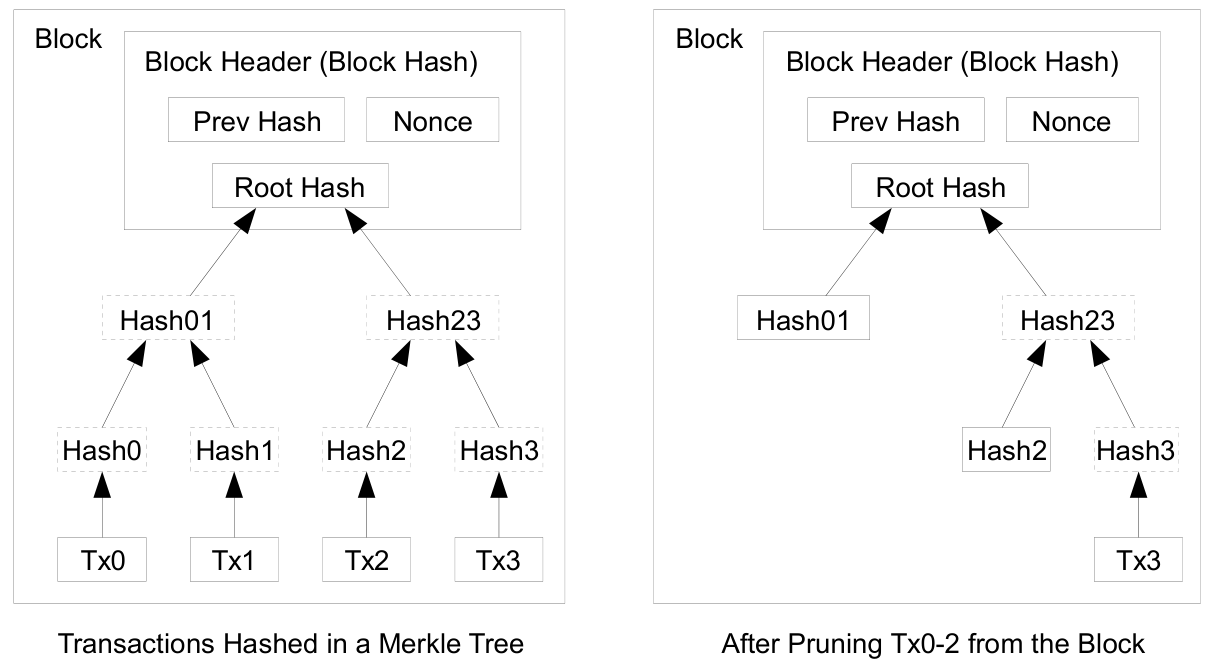
거래가 없는 블록 헤더의 크기는 약 80바이트입니다. 만약 블록이 10분마다 생성된다고 가정하면, 80바이트 _ 6 _ 24 * 365 = 연간 약 4.2MB입니다. 2008년 기준으로 컴퓨터 시스템이 일반적으로 2GB의 RAM을 제공하며, 무어의 법칙에 따르면 매년 약 1.2GB의 성장률이 예상되므로, 블록 헤더를 메모리에 보관해야 한다고 해도 저장 용량은 문제가 되지 않을 것입니다.

8. 간편한 결제 검증

전체 네트워크 노드를 실행하지 않고도 결제를 검증하는 것이 가능합니다. 사용자는 가장 긴 작업 증명 체인의 블록 헤더 사본만을 보관하면 되며, 네트워크 노드에 질의하여 자신이 가장 긴 체인을 확보했다고 확신할 때까지 확인한 후, 거래가 타임스탬프된 블록에 연결된 머클 분기를 얻을 수 있습니다. 사용자는 직접 거래를 검증할 수는 없지만, 해당 거래가 체인 내 특정 위치에 연결되었음을 확인함으로써 네트워크 노드가 이를 수용했음을 알 수 있고, 이후 추가된 블록은 네트워크가 이를 수용했음을 더욱 확증해줍니다.

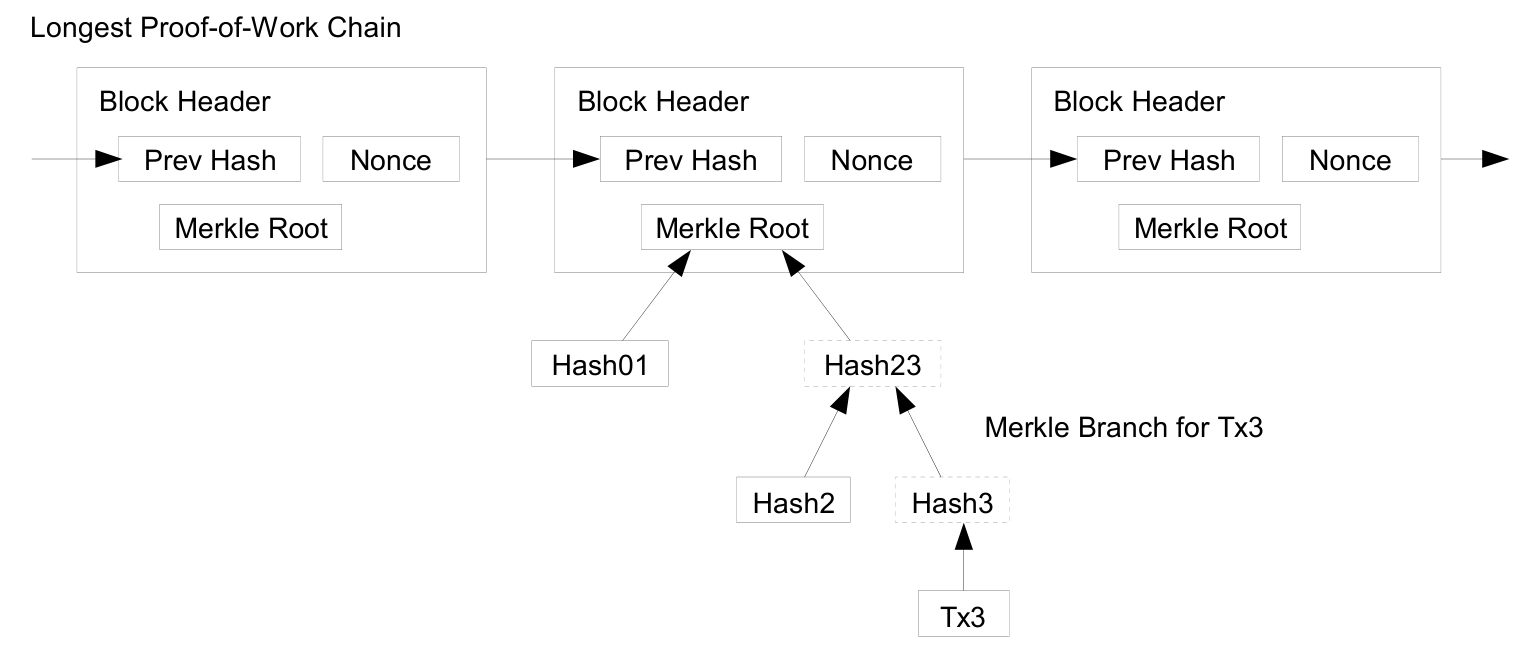
따라서 이 검증 방식은 정직한 노드들이 네트워크를 제어하는 한 신뢰할 수 있지만, 네트워크가 공격자에 의해 압도되면 취약해질 수 있습니다. 네트워크 노드들은 스스로 거래를 검증할 수 있는 반면, 간편한 방식은 공격자가 조작한 거래에 의해 속을 수 있으며, 공격자가 네트워크를 지속적으로 압도하는 한 이를 막기 어렵습니다. 이를 방지하는 한 가지 전략은 네트워크 노드가 유효하지 않은 블록을 감지할 때 경고를 수신하여 사용자의 소프트웨어가 전체 블록과 경고된 거래를 다운로드하고 일관성을 확인하도록 하는 것입니다. 빈번한 결제를 받는 기업들은 보다 독립적인 보안과 빠른 검증을 위해 자체 노드를 운영하는 것이 유리할 것입니다.

9. 가치의 결합과 분할

코인을 개별적으로 처리할 수는 있지만, 전송 시마다 각 센트에 대해 별도의 거래를 만드는 것은 비효율적입니다. 가치를 결합하고 분할할 수 있도록 거래에는 여러 개의 입력과 출력이 포함됩니다. 일반적으로, 더 큰 이전 거래에서 하나의 입력을 받거나 더 작은 금액들을 결합한 여러 입력을 사용하며, 출력은 최대 두 개로 구성됩니다. 하나는 결제 대금에 해당하고, 다른 하나는 잔액이 있을 경우 이를 송신자에게 반환하는 용도로 사용됩니다.

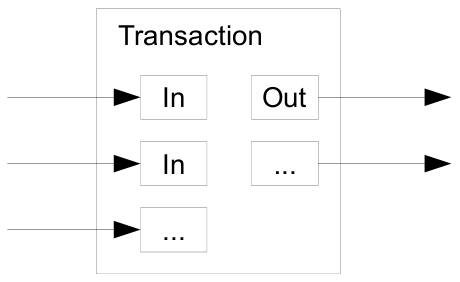
여러 거래에 의존하는 구조(fan-out), 즉 하나의 거래가 여러 거래에 의존하고, 그 거래들이 더 많은 거래에 의존하는 구조는 여기서 문제가 되지 않습니다. 거래의 전체 독립적인 기록을 추출할 필요가 없기 때문입니다.

10. 개인정보 보호

전통적인 은행 모델은 관련 당사자와 신뢰할 수 있는 제3자만 정보에 접근할 수 있도록 제한하여 어느 정도의 개인정보 보호를 제공합니다. 모든 거래를 공개적으로 발표해야 하는 필요성으로 인해 이러한 방식은 사용할 수 없지만, 정보 흐름을 다른 방식으로 차단하여 개인정보를 보호할 수 있습니다. 즉, 공개 키를 익명으로 유지하는 것입니다. 이렇게 하면 대중은 누군가가 특정 금액을 다른 누군가에게 전송하는 것을 볼 수 있지만, 거래가 특정 인물과 연결되는 정보는 없습니다. 이는 주식 시장에서 개별 거래의 시간과 규모(이른바 "테이프")는 공개되지만, 거래 당사자는 알 수 없는 정보 공개 수준과 유사합니다.

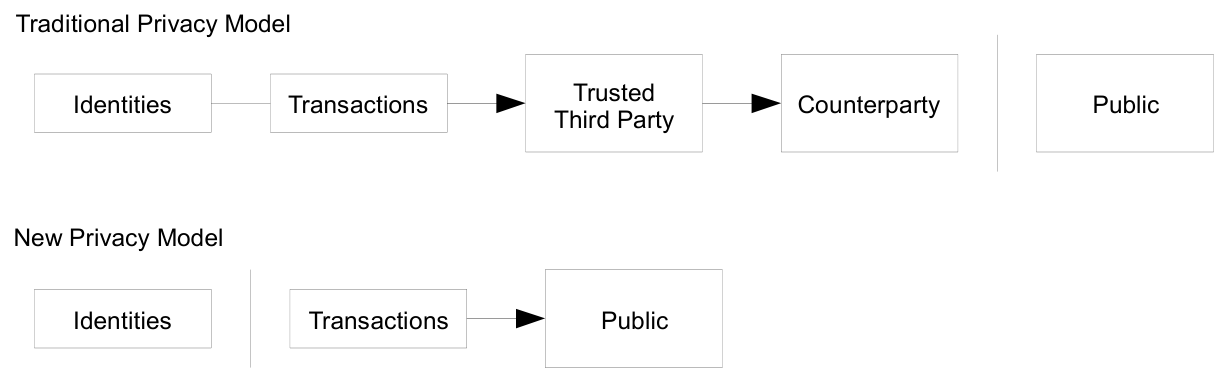
추가적인 보호 수단으로, 각 거래마다 새로운 키 쌍을 사용하여 공통 소유자와의 연결을 방지해야 합니다. 다중 입력 거래에서는 입력들이 동일한 소유자에게 속해 있음을 드러내기 때문에 일부 연결은 불가피합니다. 특정 키의 소유자가 드러날 경우, 해당 소유자의 다른 거래들이 연결되어 노출될 위험이 있습니다.

11. 계산

우리는 공격자가 정직한 체인보다 더 빠르게 대체 체인을 생성하려고 시도하는 시나리오를 고려합니다. 설령 공격자가 이를 달성하더라도, 시스템이 임의의 변경에 노출되지는 않습니다. 예를 들어, 무에서 가치를 창출하거나 공격자에게 속하지 않은 돈을 탈취하는 것은 불가능합니다. 노드들은 유효하지 않은 거래를 결제 수단으로 받아들이지 않으며, 정직한 노드는 이러한 거래를 포함한 블록을 결코 수용하지 않을 것입니다. 공격자는 오직 자신이 최근에 보낸 거래를 취소하여 돈을 되찾으려고 시도할 수 있을 뿐입니다.

정직한 체인과 공격자 체인 간의 경쟁은 이항 확률 과정(Binomial Random Walk)으로 특징지어질 수 있습니다. 성공 사건은 정직한 체인이 한 블록 연장되어 그 격차가 +1 증가하는 것이고, 실패 사건은 공격자 체인이 한 블록 연장되어 격차가 -1 감소하는 것입니다.

공격자가 특정 격차에서 따라잡을 확률은 도박사의 파산 문제(Gambler's Ruin problem)와 유사합니다. 예를 들어, 무한 신용을 가진 도박사가 적자로 시작하여 잠재적으로 무한히 많은 게임을 하면서 본전으로 돌아오려고 시도하는 경우를 생각해볼 수 있습니다. 우리가 구할 수 있는 것은 그가 본전에 도달할 확률, 즉 공격자가 정직한 체인을 따라잡을 확률입니다. 이를 다음과 같이 계산할 수 있습니다⁸.

• p = 정직한 노드가 다음 블록을 찾을 확률
• q = 공격자가 다음 블록을 찾을 확률
• q_z = 공격자가 z 블록 격차에서 따라잡을 확률

우리의 가정인 p > q 에 따르면, 공격자가 따라잡아야 할 블록 수가 증가할수록 그 확률은 지수적으로 감소합니다. 확률이 공격자에게 불리하게 작용하기 때문에, 초반에 행운의 돌진을 하지 않는 이상, 시간이 지남에 따라 공격자가 따라잡을 가능성은 극히 작아집니다.

이제 새로운 거래의 수취인이 발신자가 거래를 변경할 수 없다고 충분히 확신할 때까지 얼마나 기다려야 하는지 고려해봅니다. 여기서 발신자는 수취인이 일정 기간 동안 자신에게 지불받았다고 믿게 만든 뒤, 일정 시간이 지나면 그 거래를 자신에게 돌려주는 방식으로 변경하려는 공격자라고 가정합니다. 이런 일이 발생하면 수취인은 알림을 받겠지만, 공격자는 그 시점이 너무 늦기를 바랍니다.

수취인은 새로운 키 쌍을 생성하고 서명을 하기 직전에 발신자에게 공개 키를 제공합니다. 이를 통해 발신자가 미리 블록 체인을 준비하여 계속 작업하면서 충분히 앞서 나가기를 기다렸다가 거래를 실행하는 것을 방지할 수 있습니다. 거래가 전송되면, 부정직한 발신자는 자신의 거래에 대한 대체 버전을 포함하는 병렬 체인 작업을 비밀리에 시작합니다.

수취인은 거래가 블록에 추가되고 그 뒤에 z 개의 블록이 연결될 때까지 기다립니다. 수취인은 공격자가 어느 정도 진척했는지 정확히 알 수 없지만, 정직한 블록들이 블록당 예상되는 평균 시간을 가정하여 생성되었다고 할 때, 공격자의 잠재적인 진척도는 기대값이 다음과 같은 포아송 분포를 따르게 됩니다.

공격자가 지금도 따라잡을 수 있는 확률을 구하기 위해, 공격자가 특정 진척을 이뤘을 가능성에 대한 포아송 밀도를 해당 지점에서 따라잡을 수 있는 확률과 곱합니다.

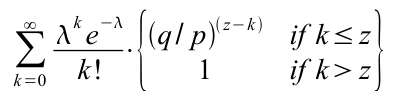
분포의 무한 꼬리를 합산하지 않도록 재배열하면...

C 코드로 변환하면...

#include <math.h>
double AttackerSuccessProbability(double q, int z)
{
    double p = 1.0 - q;
    double lambda = z * (q / p);
    double sum = 1.0;
    int i, k;
    for (k = 0; k <= z; k++)
    {
        double poisson = exp(-lambda);
        for (i = 1; i <= k; i++)
            poisson *= lambda / i;
        sum -= poisson * (1 - pow(q / p, z - k));
    }
    return sum;
}

결과를 실행하면, z 값이 증가함에 따라 확률이 지수적으로 감소하는 것을 확인할 수 있습니다.

q=0.1
z=0 P=1.0000000
z=1 P=0.2045873
z=2 P=0.0509779
z=3 P=0.0131722
z=4 P=0.0034552
z=5 P=0.0009137
z=6 P=0.0002428
z=7 P=0.0000647
z=8 P=0.0000173
z=9 P=0.0000046
z=10 P=0.0000012

q=0.3
z=0 P=1.0000000
z=5 P=0.1773523
z=10 P=0.0416605
z=15 P=0.0101008
z=20 P=0.0024804
z=25 P=0.0006132
z=30 P=0.0001522
z=35 P=0.0000379
z=40 P=0.0000095
z=45 P=0.0000024
z=50 P=0.0000006

P가 0.1% 미만이 되도록 계산합니다.

P < 0.001
q=0.10 z=5
q=0.15 z=8
q=0.20 z=11
q=0.25 z=15
q=0.30 z=24
q=0.35 z=41
q=0.40 z=89
q=0.45 z=340

12. 결론

우리는 신뢰에 의존하지 않는 전자 거래 시스템을 제안했습니다. 디지털 서명으로 구성된 코인의 일반적인 틀에서 시작했으며, 이는 소유권에 대한 강력한 통제를 제공하지만 이중 지불을 방지할 수 있는 방법 없이는 불완전합니다. 이를 해결하기 위해, 우리는 작업 증명을 사용하는 P2P 네트워크를 제안하여 거래의 공개 기록을 유지하고, 정직한 노드가 CPU 파워의 과반수를 통제하는 한 공격자가 이를 변경하는 것이 계산적으로 불가능하도록 만들었습니다. 네트워크는 비구조적 단순성 속에서 견고합니다. 노드들은 거의 조정 없이 동시에 작업을 수행하며, 특정 위치로 메시지를 라우팅할 필요 없이 최선의 노력으로만 전달되면 됩니다. 노드는 언제든지 네트워크에 떠나고 다시 합류할 수 있으며, 그동안 발생한 사건에 대한 증거로 작업 증명 체인을 받아들입니다. 각 노드는 CPU 파워로 투표하며, 유효한 블록을 확장함으로써 이를 수용하고, 유효하지 않은 블록은 작업을 거부함으로써 배척합니다. 필요한 규칙과 인센티브는 이러한 합의 메커니즘으로 시행될 수 있습니다.

Footnotes

1. W. Dai, "b-money," http://www.weidai.com/bmoney.txt, 1998. ↩

2. H. Massias, X.S. Avila, and J.-J. Quisquater, "Design of a secure timestamping service with minimal trust requirements," In 20th Symposium on Information Theory in the Benelux, May 1999. ↩ ↩²

3. S. Haber, W.S. Stornetta, "How to time-stamp a digital document," In Journal of Cryptology, vol 3, no 2, pages 99-111, 1991. ↩

4. D. Bayer, S. Haber, W.S. Stornetta, "Improving the efficiency and reliability of digital time-stamping," In Sequences II: Methods in Communication, Security and Computer Science, pages 329-334, 1993. ↩

5. S. Haber, W.S. Stornetta, "Secure names for bit-strings," In Proceedings of the 4th ACM Conference on Computer and Communications Security, pages 28-35, April 1997. ↩ ↩²

6. A. Back, "Hashcash - a denial of service counter-measure," http://www.hashcash.org/papers/hashcash.pdf, 2002. ↩

7. R.C. Merkle, "Protocols for public key cryptosystems," In Proc. 1980 Symposium on Security and Privacy, IEEE Computer Society, pages 122-133, April 1980. ↩

8. W. Feller, "An introduction to probability theory and its applications," 1957. ↩